Cuando una persona está resolviendo un examen va donde el profesor cada rato y pregunta y pregunta acerca de un problema, hasta se olvida que esta rindiendo un examen, después dice, esta mal planteada la pregunta, y raja, se molesta, tira la silla y sale del examen y comenta con sus compañeros e insiste que el problema estaba mal planteado, lógicamente que eso puede suceder; si para usted es todas las veces así, quizás resulte que en el examen que acaba de desaprobar y después que el profesor resolvió el problema usted diga ¡claro la pregunta era esa!, ¡verdad esa era la respuesta!. En el colegio también lo hacíamos.
¡La experiencia enseña!, habemos personas que intentamos dar respuestas a los problemas, sin haber entendido de lo que se trata, algo así como que al leer o escuchar, leemos o escuchamos a medias y si en esta situación nos encontramos pues lo que estamos haciendo es aumentar la dificultad del problema, que se supone vamos a solucionar. Ante un problema, hay que leer o escuchar cuantas veces sean necesarias, hasta comprender o memorizar el enunciado si fuera posible.
Cuantas veces hemos fracasado por no escuchar o saber leer bien, lo que implica entender. Saber escuchar o leer es saber comprender. ¡Si no entiende un problema no se atreva a resolverlo, mejor quédese intentado comprenderlo!
A continuación planteamos 3 pasos indispensables en el desarrollo de problemas usando algoritmos.
PASOS PARA DEFINIR PROBLEMAS
1. COMPRENDER EL PROBLEMA:
Lea o escuche atentamente el problema. Haga un bosquejo, tantee una posible solución. Si no entiende el problema no continúe al paso 2.
2. IDENTIFICAR LAS ENTRADAS, PROCESOS Y SALIDAS
Entradas: Identifique los datos de ingreso al algoritmo.
Procesos: Son las operaciones, cálculos matemáticos o procesos que se realizan con los datos de entrada, a veces dependen del conocimiento de algún tema especifico, puede ser matemáticas, estadística, química, biología, investigación de operaciones, contabilidad, etc.
Salidas: Son los resultados a imprimirse o mostrarse. Es la solución al problema. Son las respuestas.
3. COMPROBAR:
Consiste en simular para verificar si el algoritmo resuelve el problema realmente, se hacen con los datos posibles de entrada, puede realizarse en papel y a mano.
Generalmente los problemas con estructuras secuénciales y selectivas son más complicados de comprender y fáciles de identificar las entradas, procesos y salidas, ya que las soluciones tratan de al menos de operaciones matemáticas u procesos sencillos. Por otro lado los problemas donde se usan bucles o repeticiones, son sencillos de comprender y difíciles de identificar las entradas, procesos y salidas.
EJEMPLO 1: Escribir un algoritmo para un programa que calcule el área de un trapecio.
1. Comprendiendo el problema:
Luego de saber que el problema se trata de geometría y es un tema que todo estudiante de educación superior conoce, el problema ya estaría comprendido de antemano, específicamente se trata del cálculo del área de un trapecio.
2. Identificando las entradas, procesos y salidas
Entradas: Para calcular el área de un trapecio, necesitamos saber el valor numérico de: la base mayor, base menor y su altura.
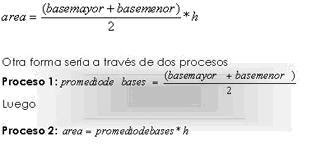
Procesos: El proceso general a realizarse sería:
Salidas: La única salida sería el , en ambos casos

Algoritmo
Inicio
Declare area, basemayor, basemenor, altura
Area: ((basemayor+basemenor)/2)* altura
Imprimir area
Fin